The Square Root of the Square Root of -1

So your precalculus teacher tells you the square root of -1 is i. Did you ever ask her what the square root of i is? You'll either get a dirty look or an interesting exploration into complex numbers that will probably last twenty minutes into your lunch block.

As I said in the previous post, mathematicians learned they'd have to deal with the square roots of negative numbers as if they were just another letter in algebra. Eventually they reasoned that multiplying by -1 was like a 180 degree rotation around 0. Well, what if you did that in 2 steps?

The vertical axis was renamed the imaginary axis, so complex numbers like a + bi could be expressed as points. Multiplying by the square root of negative one will get you halfway around, then multiplying again will get you the full 180 degrees. So multiplying by the square root of -1 is like a 90 degree rotation.

But what about the square root of i? That can be solved in a similarly geometric fashion. Just make the 90 degree rotation in two steps, each one being the square root of i. And each step will be a 45 degree rotation:

Using the 45-45-90 special triangle formula, the point is 1/sqrt(2) in the horizontal direction and 1/sqrt(2) in the vertical direction. 1/sqrt(2) is around .7071, and if you square 1/sqrt(2) + i/sqrt(2) you'll get i.

(1/sqrt(2) + i/sqrt(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i - 1/2 = i

Actually, if you did a rotation of 225 degrees twice you would rotate all the way around and back to 90 degrees, so that gives another square root of i.

Trig Identities

After working with a student whose teacher has been covering trig identities for weeks (!), I was lucky enough to stumble on the way those abstract exercises were invented.

Trig functions (sine, cosine and tangent) are ratios of the sides of a right triangle, and there are certain relationships between them that can be exploited for fun and profit. For example, (sinA)² + (cosA)² = 1, so you can replace (sinA)² with 1 - (cosA)².

In the days before calculators, it was useful to be able to find the trig function of an angle just by knowing the function of a related angle, like half of A. These "double angle" formulas can be derived using a little algebra and geometry and are still trotted out in the 21st century:

sin2A = 2sinAcosA and cos2A = 2(cosA)² - 1

I can see some value in not wanting to do integration on a function involving a square or a product, so being able to substitute a straight double angle function might be preferable. Of course, trig identities are taught long before calculus, so I have no idea what reason precalculus teachers give for still teaching them, other than they're (at best) interesting brainteasers.

The trig identities my student was being asked to prove were for larger angles, like 3A and 4A, requiring more algebra, and departing ever more from real applications. I wondered how mathematicians were able to discover a relation like cos4A = 8cos⁴A - 8cos²A + 1. Elsewhere, I've shown how we proved this identity using cos2A = 2(cosA)² - 1 but after weeks of sleepless nights and cornea-searing research I finally found the mysterious trig identity generator.

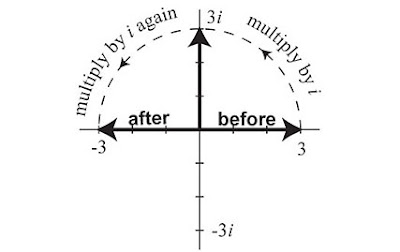
Once mathematicians discovered how to deal with crazy numbers like the square root of -1 using algebraic shorthand, they quickly started playing around with coordinate systems to visualize the strange numbers.

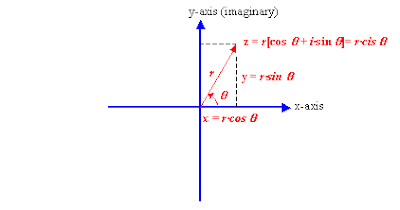
As you can see in the figure above, any point can be expressed as r(cosA + i sinA) or rcisA. It seems like a long-winded way to express a number like (3, 4) or 3 + 4i, but the trig form has the advantage of being able to multiply, divide and take complex numbers to any exponent very easily. De Moivre's Theorem is the shortcut:

r₁cisA * r₂cisB = r₁r₂cis(A+B)

r₁cisA / r₂cisB = (r_1/r₂)cis(A-B)

and most importantly, (rcisA)ⁿ = rⁿ (cos(nA) + i sin(nA))

Easy, huh? For example, taking r = 1 and n = 4:

(cosA + i sinA)⁴ = cos(4A) + i sin(4A)

This can be made easier using Pascal's Triangle to help expand (a + b)⁴:

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

Now replace a with cosA and b with i sinA:

cos⁴A + 4cos³A i sinA + 6cos²A i² sin²A + 4cosA i³ sin³A + i⁴ sin⁴A

so cos(4A) + i sin(4A)

= cos⁴A + 4cos³A i sinA - 6cos²A sin²A - 4cosA i sin³A + sin⁴A

The real part of the left side of the equation must equal the real parts of the right side:

cos(4A) = cos⁴A - 6cos²A sin²A + sin⁴A

Now replace sin²A with 1 - cos²A:

cos(4A) = cos⁴A - 6cos²A (1 - cos²A) + (1 - cos²A)(1 - cos²A)

cos(4A) = cos⁴A - 6cos²A + 6cos⁴A + 1 - 2cos²A + cos⁴A

cos(4A) = 8cos⁴A - 8cos²A + 1

And that's how those sneaky mathematicians generated the identity my student and I worked so hard to prove. Next time: i is the square root of -1, but what is the square root of i??

Did Euclid Exist?

When I was researching the course that became the Fun Calculus Program I googled "calculus without limits" and found the website of C.K. Raju, award-winning Indian physicist, mathematician and author. Having my idea of teaching a quick, pragmatic calculus course scooped by one of the guys responsible for developing Param, India's supercomputer, wasn't such a disappointment. I figured I still had his five-session course beat in terms of historical context, but, not surprisingly, Dr. Raju has some earth-shaking ideas about the history of mathematics, too.

Raju's paper Towards Equity in Mathematics Education 1.Good-Bye Euclid! explores the suspiciously few facts that have come down to us about the Father of Mathematics himself, Euclid. The main mention of Euclid was by 5th century philosopher Proclus, and our sources for Proclus are dated at least five hundred years after he died. Raju teases us with the suggestion that the Elements may have been a product of Eastern-influenced philosophy the Church found uncomfortable.

So while the Church and its flock busied themselves burning books and lynching scholars like Hypatia, the Arabs created vast libraries, preserving, translating and developing the ideas in Greek philosophy and science.

"However, as Adelard of Bath, one of the first translators of the Elements, remarked, Muslims accepted reason, while authority prevailed in Christian Europe."

It has come down to us (including my high school history class) that the Arab libraries were simply a huge Public Storage location keeping "our" knowledge safe until we Europeans were ready to reclaim it. In popular culture James Burke's Day the Universe Changed was unique in suggesting the Muslims actually made use of this knowledge and Burke pointed out elsewhere that the universities of Paris (1150), Bologna (1088) and Oxford (1096) were founded, coincidentally, only a few years after the arrival of European translators to the dozens of libraries of Toledo ("liberated" in 1085).

One of the accidental products of this flurry of translation was the creation of the trigonometric term "sine" by over-literal translators. Another may have been the birth of Euclid. Raju tries to trace the etymology of the name itself:

Possibly, the name “Euclid” was inspired by a similar translation error made at Toledo regarding the term uclides which has been rendered by some Arabic authors as ucli (key) + des (direction, space). So, uclides, meaning “the key to geometry”, was possibly misinterpreted as a Greek name Euclide.

It's a fascinating possibility. We mathematicians like to believe we have a personal relationship with Euclid; how could he not have existed?

Raju's works are full of such thought-provoking perspectives. I agree with him that the Western idea of proof is a religious one; the above statement that authority prevailed in Europe is no less true in mathematics. Having thrown off religious authority, math still seems to need the comforting authority of proof.

The Hunt for e

After a quick mini-course in Trigonometry during Monday's meeting of the Fun Calculus Program, the next installment will trace the discovery and development of the transcendental number e, which is around 2.7. My historical approach is of course influenced by Eli Maor's brilliant book e, Story of a Number, which explores e and its connection to logarithms, calculus, spirals and infinite series in fascinating detail.

I'm in the process of finding precalculus or calculus teachers who will allow me to observe their classes, because if textbooks are any indication, e is introduced as casually as breadsticks are plunked down on your table at Olive Garden. My suspicion is that most math teachers aren't aware of the rich history and applications that would make e more accessible and memorable. Even if teachers are aware, I'm sure entertaining such frivolous pursuits would cut into the time spent teaching 18th century tasks like estimating the roots of a polynomial.

The truth is "The Hunt for e" was a real issue in the 1600s, after Fermat and others had figured out the pattern for finding areas under curves. The one curve that defied analysis was the hyperbola y = 1/x or x^-1, since using the area pattern would cause a zero denominator, which still frightens mathematicians in the 21st century. The curve definitely had an area underneath it, but finding a function to express it seemed impossible.

No less a genius than Newton took up the task and showed his skills by extending Pascal's triangle in a completely unexpected direction! He used his new invention, Calculus, to find an infinite series for the area under the hyperbola (a great way for a calculus teacher to introduce the need for such a seemingly unrelated idea) and was able to calculate the area with great precision.

Finding an actual function for the area took a similar step of logic, and many mathematicians had already noticed the area had a logarithmic quality: the area up to 2 plus the area up to 3 equals the area up to 6. Adding to multiply? How Scottish! After 20 years of painstaking drudgery performed by the Laird of Murchiston (who took time out of his busy schedule publishing Anti-Catholic propaganda to invent logarithms), astronomers and mathematicians were equipped with the 17-century equivalent of a TI-84. And they recognized the hyperbolic area problem as one of exponents. But what was the base of the exponents?

A seemingly harmless number already calculated by a bored banker who wondered how much money you'd make if you invested $1 at 100% interest for a year, compounded continuously.

It was the "compounded continuously" part that made e a most useful number for calculating populations (of people, animals and bacteria), temperatures, and in a few hundred years, amounts of radioactive material.

Quite a story!