But now it's 2014 and students are still multiplying matrices by hand and are never getting to see their transformational power. I say that literally because matrices are used to transform (rotate, reflect, translate) points in a 2 or 3-D plane. What would video games be without rotation matrices? That's right: Pong.
Unfortunately many textbooks neglect this graphical application which could be used to grab students' attention. Good for us Don "The Mathman" Cohen didn't neglect it. On the contrary, he and his very young students graphed a simple "dog" and multiplied its points one by one and graphed the result. Their work can be found in Cohen's characteristically clear, engaging and thought-provoking book "Changing Shapes with Matrices."
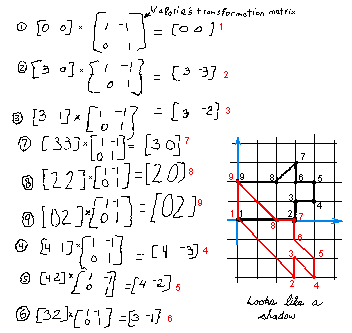
When I was working with a homeschooled Algebra 2 student on matrices, we used Python and its professional-strength numerical package Numpy to multiply and transform our matrices.
But if you're just using a 2x2 transformation matrix, it's not hard to write your own functions in Python to draw and multiply matrices. Since I don't have to do the multiplying by hand, I can use more points than Cohen did. I chose to transform a big F since it has no rotational or reflective symmetry and my last name starts with F. First draw it on graph paper (or Geogebra) to get the points:
Now type the points into an n x 2 matrix:
Ok, it's just a list. But we're using our imagination here. Now enter your favorite transformation matrix:
The above code isn't obvious. i needs to go up by 2 in order to skip from point to point, and j only has 2 values. But the a[i]*b[j] line is especially guaranteed to challenge math students! It'll make them think about how you multiply matrices, that's for sure:
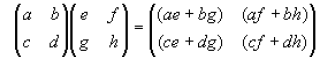
Now just have the program multiply the F-matrix by the transformation matrix and graph the result:
Notice the new x-value is the old y-value and the new y-value is the negative of the sum of the old x- and y-values. I think this is exactly the kind of exploration math students should be getting so they can experience transformations and matrices first hand. I suspect this can all be done with a couple of keystrokes in IPython but doing some real programming to multiply matrices and graph the result is a great exercise!




















