Crypto-Code

A student of mine was thinking out loud about encoding messages and it got stuck in my head. The next day I challenged my Coder School students to try it. How do you even replace a letter with a number? You could use dozens of if-statements:

for letter in message:
    if letter == 'a':
        print(1)
    elif letter == 'b':
        print(2)

And so on. But an easier way is to create a string of characters:

ALPHA = "abcdefghijklmnopqrstuvwxyz ',.?"

Now each letter has a number, an index, its place in the string. The letter a is ALPHA[0], b is ALPHA[1] and so on . You can replace each letter with its index this way:

def encode(msg):
    '''takes a message and prints number code'''
    for letter in msg:
        print(ALPHA.index(letter), end=' ')

The last bit is thanks to Python 3, where print is a function. After printing the number you can specify printing something at the end, like a space. And it doesn't automatically print a line break. Running encode('call me ishmael.') we get

2 0 11 11 26 12 4 26 8 18 7 12 0 4 11 28

The decode function will require a little Python trickery. The numbers can be fed back in as a list if you're patient enough to type tons of commas, or it can be copied and pasted in, as a string inside quotes, to a function like

decode('2 0 11 11 26 12 4 26 8 18 7 12 0 4 11 28')

The decode function converts the string to a list using Python's split() function. Then you can just iterate over the list, printing the letter in the ALPHA list with that index number.

def decode(msg):
    '''takes numbers and prints decoded letters'''
    msg2 = msg.split() #converts string to list
    for item in msg2:
        print(ALPHA[int(item)],end = '')

So decoding another message, like

decode('8 26 22 0 13 19 26 19 14 26 7 14 11 3 26 24 14 20 17 26 7 0 13 3 28')

we get 

i want to hold your hand.

But that cipher wouldn't fool spies even from a thousand years ago. We need to make it a little sneakier. We could get rid of the spaces if all the numbers were 2-digits long:

def encode(msg):
    '''takes a message and returns number code'''
    code = ''
    for letter in msg:
        #get the index of letter and
        #convert it into a string
        num = str(ALPHA.index(letter))
        if len(num) == 1: #if it's only one digit
            num = '0' + num #add a zero in front
        code += num         #add that to the code
    print(code)

Now execute encode("beautiful is better than ugly.") and you'll get a more confusing-looking code:

010400201908052011260818260104191904172619070013262006112428

Now decoding it is fairly simple. You just have to take 2-digit slices from the string and print out the element of ALPHA that has that index.

def decode(msg):
    '''takes numbers and prints decoded letters'''
    for n in range(0,len(msg),2): #n goes up by 2's
        print(ALPHA[int(msg[n:n+2])],end='') #take 2-digit slices

Your enemy might notice a bunch of zeroes. My student's suggestion was to convert to binary numbers, make all the numbers 5-digits, then string them together! I already have a binary converter in my book Hacking Math Class, so we'll assume you have the binary function. You've converted the letters to numbers, then send them to this function:

def binary5(number):
    '''converts number to 5-digit binary'''
    number = binary(number) #get the binary form
    number = str(number) #convert to string form
    x = len(number)     #to find number of digits
    number = (5-x)*'0' + number #add zeroes if it's not 5
    print(number)

Now entering binary5(5) will add zeros to the front to make it a 5 digit number:

00101

I created strings of even and odd numbers for random choosing:

EVENS = '02468'

ODDS = '13579'

Here's the code (instead of printing) for converting the zeros to any even digit and the ones to any odd digit:

    #convert to random evens and odds
    binrand = ''     #string for random evens or odds
    for digit in number:        #go over every character
        if int(digit) % 2 == 0: #if its integer form is even
            #replace with random even digit
            binrand += random.choice(EVENS)
        else: #otherwise, replace it with random odd digit
            binrand += random.choice(ODDS)
    return binrand

Here's the new encode function:

def encode(msg):
    '''takes a message and returns number code'''
    code = '' #empty string for numbers
    for letter in msg: #goes over every letter
        #take the index of that letter, convert to
        #5-digit binary and add that to number string
        code += binary5(ALPHA.index(letter))
    print(code)
    print()#blank line

Now running the encode function will encode our message nicely.

>>> encode("what's my age again?")
9217424331466441621919055700927185047984178469303480480845780254853858208286417028442012044592133956

The first 5-digit slice, '92174', using the evens = '0' and odds = '1' transform, is the binary number 10110. That's 22 in decimal, or w's place in the ALPHA string.

The decode function reverses the process. First it takes the message and slices it into 5-digit slices.

def decode(msg):
    '''decodes a message'''
    msg2 = [] #list for 5-digit numbers
    for n in range(0,len(msg),5): #n goes up by 5's
        #add each 5-digit slice to list
        msg2.append(int(msg[n:n+5]))

Then it creates a list to store the 5-digit binary numbers and converts all the even digits to zeros and all the odds to ones.

    msg3 = [] #list for 5-digit binary numbers
    for number in msg2:
        number2 = str(number) #turn it into a string
        number3 = ''        #empty string for binaries
        for digit in number2: #go through digit by digit
            if digit in EVENS: #if digit is even
                digit = '0'         #replace by 0
            else: digit = '1'       #or replace by 1
            number3 += digit        #add to binary string
        msg3.append(number3)        #add binary string to message
        #print(msg3)

Finally you have to convert all the binary numbers to decimals. It's a good thing leading zeros are ignored by Python's 'int' function. That saves us a step. I already have a function for converting binary to decimal, (called "binDec") so I didn't give the code here.

    for number in msg3:     #go through binaries
        #convert to int, then decimal, then letter:
        print(ALPHA[binDec(int(number))],end = '')
    print()             #blank line after message

Now entering a nonsensical string of unbreakable code will yield a message of power and beauty:

>>> decode('164732271528482768355715312256534944844083853656139
161595498463010797645033218905045253958')
that's all, folks!

Update: Naturally my Python mentor Paddy Gaunt showed me how to do it in an eighth of the code.

import numpy as np

ALPHA = "abcdefghijklmnopqrstuvwxyz ',.?"
ALPHA = {c:i for i,c in enumerate(ALPHA)} # make it into a dict

def encode(str):
    narr = np.array([ALPHA[c] for c in str], dtype=np.uint8)
    narr = np.unpackbits(narr).reshape(-1, 8)[:,3:].reshape(-1)
    evod = np.array([np.random.choice([0,2,4,6,8], len(narr)),
                     np.random.choice([1,3,5,7,9], len(narr))])
    return evod[narr, np.arange(len(narr))]


print(encode("the quick brown fox jumps over the lazy dog"))

Boring Stuff, Automated

Thanks to Al Sweigart for the title to his latest Python book. Automating the boring stuff is reason enough to learn a bit of programming. Here's how I used Python to automate something boring today.

Every week or so in my new teaching job I have to time students one by one as they write strings of symbols. The way it's usually done is with a stopwatch, and the student pauses to write down the time for each of the 25 trials. Since I was looking at testing all my students this week, I wondered if I could write a Python program that would help.

This summer I worked at a camp introducing Python programming using Pygame and I've been keeping up my skills. Many of the programs involve interaction with the keyboard or mouse and I woke up this morning with an idea to write a stopwatch program using the space bar. I fired up the Pygame template I adapted from Professor Craven of Simpson College. First I had to create a list to store all the times, and create a variable to tell when the program is timing or not.

Then I just added to the usual key-events code where Pygame checks if the user clicked to exit the program or pressed a key. Here's the code for "if the space key is pressed and if you're not timing, record the present time and start timing (and print "timing" in the shell so I'll know)."

But if the program is already timing, record the present time, calculate the elapsed time, and add that to the times list. If the times list is 25 items long, stop the program.

I like that last line. Whenever the space bar is clicked, it toggles between timing and not timing.

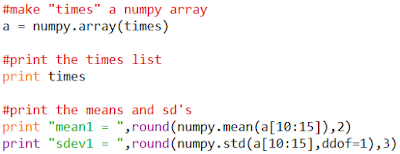
Here Comes Numpy

The tedious part is calculating the means and standard deviations of 3 blocks of times. Most teachers type the numbers into a web page, but since we've already got the times in a list I knew it would be child's play to get the means and standard deviations. All I needed to do was to make the times into a Numpy array and use the "mean" and "std" functions.

Here's what the final result looked like.

The students were impressed I could produce their results so quickly!

Finally Some Class

When I started learning Python a few years ago I was confused about when classes were needed. Books and websites were no help (this gem is from python.org):

class Dog:
    kind = 'canine'
    def __init__(self,name):
        self.name = name

This makes absolutely no sense to me. Why the need for a Dog class?

Balls to the Rescue

So I avoided the whole subject; I wrote a book on learning math using Python and never needed to use a class. Let me go out on a limb here. The only time the beginning programmer is going to need a class is when they will be creating a bunch of related objects. Like balls in a game program.

I like to learn and teach programming through creating cool graphics, and a good early project is a Pong clone. Just making a ball bounce around the display window is a challenge that pays off visually when it finally works. Here's the code for one ball in Pygame:

#import modules 
import pygame 
from pygame.locals import *

#define some colors
BLACK = (0,0,0)
WHITE = (255,255,255)
GREEN = (0,255,0)

#ball's initial position
xcor = 100
ycor = 100

#ball's velocity
xvel = 2
yvel = 1

#ball's diameter
diameter = 20

#set up display 
pygame.init() 
screen = pygame.display.set_mode((600,500)) 
pygame.display.set_caption('insert caption here!') 

#loop until the user clicks the close button 
done = False 

# Used to manage how fast the screen updates
clock = pygame.time.Clock()

while not done: 
    for event in pygame.event.get(): 
        if event.type == QUIT: #if pygame window is closed by user
            done = True #stop the loop
    
    #first make the background black
    screen.fill(BLACK)

    #check if the ball is off the screen
    if xcor > 0 or xcor > 600 - diameter:
        xvel = -xvel #make it go the opposite direction
    if ycor > 0 or ycor > 500 - diameter:
        yvel = -yvel #make it go the opposite direction

    #update the ball's position
    xcor += xvel
    ycor += yvel
    
    #draw the ball
    pygame.draw.ellipse(screen,WHITE,
                            [xcor,ycor,diameter, diameter])
     
    #update the screen 
    pygame.display.update()

    #set the speed
    clock.tick(120) 

#Quit nicely 
pygame.quit()

And here's our ball, bouncing around nicely:

But in order to make another ball, you'd have to copy a bunch of code and keep track of "xcor1" and "yvel2" and so on. Three balls would be the beginnings of a headache and 10 balls would be out of the question. But what if there was a way to create as many balls as you want, each with its own size, color, location and direction, just by changing one number in your code? I'm all ears.

That's the reason to use classes. We've already written code for the moving and bouncing, all we need to do is copy that code into a Ball class to make it magic:

class Ball():
    def __init__(self,xcor,ycor,xvel,yvel,color,diameter):
        self.xcor = xcor
        self.ycor = ycor
        self.xvel = xvel
        self.yvel = yvel
        self.color = color
        self.diameter = diameter
        pygame.draw.ellipse(screen,self.color,
                            [self.xcor,self.ycor,
                             self.diameter,self.diameter])

    def move(self):
        if self.xcor < 0 or self.xcor > 600 - diameter:
            self.xvel = -self.xvel
        if self.ycor < 0 or self.ycor > 500 - diameter:
            self.yvel = -self.yvel
        self.xcor += self.xvel
        self.ycor += self.yvel
        pygame.draw.ellipse(screen,self.color,
                            [self.xcor,self.ycor,
                             self.diameter,self.diameter])

Now thanks to loops, we can create a bunch of Balls, put them into a list and just iterate over the list to move the balls. In this code the position, velocity, color and size of each ball is randomly generated.

#create the balls
for i in range(60):
    newball = Ball(randrange(0,700),  #x-coordinate
                   randrange(0,500),  #y-coordinate
                   randrange(-10,10), #horizontal velocity
                   randrange(-10,10), #vertical velocity
                   choice(colors),    #color
                   randrange(5,50))   #diameter
    ball_list.append(newball)         #add it to the ball list

And all the movement code in the one-ball program is replaced by the very simple

    #move the balls
    for ball in ball_list:
        ball.move()

And this is the result, which you'll have to imagine moving gracefully:

Want more or less balls? Just change the number in the "for i in range(60)" line.

And that's the right way to introduce classes in programming.

Limit of Sigma? Python to the Rescue!

I got an email today from a college student I tutor:

Hey Peter, there's a problem in the sigma notation section to find the limit as n goes to infinity, i=1 ending at n that goes like: 2/n((2i/n)^3+5(2i/n)). Please help! Thank you.

Translating a complicated problem into an email isn't easy. This is how the problem looks in a textbook:

It's been a long time since I forced myself to solve sigma problems by hand, so the first thing I did was set up a Python program to make i go from 1 to n and return the sum:

Python 2 will round this off to whole numbers, so I added the "from __future__" line to tell it to use decimals. I discuss this in my book Hacking Math Class with Python. 

Now I ran the program and made n a million. It's not infinite, but it should give an idea of what the sum is as n gets really large.

Looks like it gets really close to 14. The algebraic solution requires that we separate the n's and the i's. 

At this point you can replace the sigma-i's with their equivalent expressions in n. It's in every calculus book:

Making the substitutions and slogging through the algebra:

 Now we can stop and let n get really large. That will just make all the terms with n's in the denominator get really small. We can replace them with 0's.

4(1 + 0 + 0) + 10(1 + 0)

4(1) + 10(1)

14

As usual the algebraic solution is six times as long as a numerical solution using a short computer program. Thanks, Python!

Cooking Up Pi

Happy Pi Day! One day out of the year we math geeks get to show off some Pi-related trivia we've dug up. Personally I love the artsy, the musical and even the food-related Pi-ponderings out there. But I'm a "Pi-thon guy" and I'm interested in the techy aspects of Pi Day.

Everybody knows Pi is the ratio of the circumference of a circle to its diameter. The Greeks were surprised that a nice perfect 1-unit wide wheel didn't roll out a beautiful whole number in one rotation. It always rolled just over 3 units. 3 and a half? Not even close. 3 and a quarter? Not quite. 3 and an eighth? Pretty close. 3 and a seventh is a good approximation, and in textbooks for centuries 22/7 stood in as the simple version of pi.

2,000 years ago Archimedes used the ratio of the perimeter of a 96-sided polygon to its diameter to get a really accurate approximation: between 3 + 10/71 and 3 + 10/70. Around 3.14185

About 600 years later in China, Zu Chongzhi used a 12,288-sided polygon (!) to improve the approximation to 3.1415929. How good is this approximation for all practical purposes? Well, the orbit of Jupiter is pretty close to a circle with a radius of 483,800,000 miles. So the 3 ten-millionths of error in Zu's value of pi corresponds to about 240 miles in arc of the orbit of Jupiter.

But at this very second a bunch of supercomputers somewhere are cranking out millions and millions more digits of pi. How do we get so precise? A history lesson is in order.

A few years ago some lucky homeschoolers attended my Math Through Technology course and they learned how Issac Newton extended Pascal's Triangle backwards (!) to get a formula for

(a + b)ⁿ

when n is negative. It was an infinite series that worked for numbers less than 1:

1/(1 + x) = 1 - x + x² - x³ + ...

When the methods of Calculus got out, mathematicians found a formula for the derivative of the arctangent of a number:

(d/dx) atan(x) = 1/(1 +x²)

Looks similar! We can just replace x with x² , integrate the terms one by one and we have an infinite series for arctangent:

(d/dx) atan(x) = 1/(1 +x²)

(d/dx) atan(x) = 1 - x² + x⁴ - x⁶ + ...

If you've ever gotten up to Precalculus or Trigonometry you might wonder why all of a sudden they stop using degrees and start using radians. It's actually supposed to make finding arc lengths easier, but it can be confusing to see all those pi's. For example, instead of 45 degrees, you say "pi/4". The tangent of 45 degrees, I mean pi/4, is 1, so the arctangent of 1 is pi/4. The European mathematicians thought they were so bright in changing their series to:

Just add up a few fractions, multiply by 4 and we clever Europeans have pi to as many places as we want! Two problems: this formula was already well known to the folks in India (perhaps the Jesuits brought it back?) and it converged so slowly that it was almost useless. I illustrate this in my book Hacking Math Class Using Python. You can write a Python program to use a certain number of terms to calculate pi using the series:

Only 2 correct decimal places after 1,000 terms? A better series was needed. In the 1700s John Machin was playing around with tangent formulas. He started with the 45-degree right triangle. The tangent here is 1.

Machin inserted 4 triangles with a tangent ratio of 1/5 and nearly got to pi/4:

It was just a tiny bit off. Some tangent formulas made it easy to calculate just how far off.

Machin's improvement on the pi formula is as follows:

In Hacking Math Class I show you how to adapt the Python code above to return the arctan and then call it from a "machin" function.

def arctan(x,depth):
    x = float(x)
    runningSum = 0
    for i in range(depth):
        term = (-1)**i*(x**(2*i+1)/(2*i+1))
        runningSum += term
    return runningSum

def machin(depth):
    return 4 *( 4*arctan(1./5.,depth)- arctan(1./239.,depth))

Now using only 10 terms of the series (not an unreasonable amount of effort for an 18th century mathematician), we get 10 correct digits of pi!

Of course in the centuries since Machin there have been many more series found to approximate pi. Check them out on Wolfram Mathworld and code them in Python!

Hacking Math Class: The Book

It seems like a century ago I learned from Seymour Papert that everything worth doing in math can be done using a computer. I learned enough Logo to make turtles walk around a screen and make geometrical figures, and I knew I was onto something every math student could use. After that every math class I taught had a computer component, much to the confusion of administrators and even my fellow math department members.

Years later I learned Python so I could help a computer-philic homeschooled kid explore math topics by writing programs. He excelled and his family was very supportive of my methods. I kept all the explorations we did and was inspired to do more exploring on my own.

The outcome of all this activity is Hacking Math Class With Python: Exploring Math Through Computer Programming, a 130-page book available for download on my website. It starts with an introduction to the Python programming language and its excellent turtle module. Those hardworking turtles are made to do everything from simple geometry to graphing polynomials to drawing fractals to transforming figures using matrices. Unique in its approach to math education, the book contains all the code necessary to explore math topics from arithmetic to differential equations.

Derivatives? Integrals? There are explorations in the book to help visualize Calculus problems and to show how easy it is to find numerical solutions. Vectors? They're the key to interactive graphics and animation, so why not have students write programs to make objects fly around the screen?

Every math textbook has a picture of a Mandelbrot Set, but until now none would actually teach the reader to draw one. That's because it would take you a year to iterate all those complex numbers without a computer. Hacking Math Class leads you step-by-step through the program.

Python is an excellent first language to learn, and there are plenty of people making a fine living programming in Python. The book presents the basic tools of programming and shows how powerful those tools can be. The reader is expected to install Python and code along. It's not "easy," but it rewards a bit of effort! Enjoy.

Hail to the Exec

Today a student in my Python programming class was working on printing out letters on a set of 4 blinkytapes. He'd already spent a lot of time defining functions for how to print out each letter of the alphabet. He called the functions "letterA()" and "letterB()" and so on. Now he wanted to print out whatever the user types in. It's easy to get input from the user:



Then you can loop through the "word" letter by letter:

But the question is how to execute the "letterA()" function when the user types in "a." He was going to use a long list of if statements (he figured copying and pasting would save him a lot of typing) but as usual Python has an easier way.

exec()

There's a function called "exec" which will execute the code inside the parentheses. So my student could put some strings in the argument:

This means he should have just called his functions "a()" and "b()" and so on. But instead of having him change every function name, I suggested he put in this code:



This changes the letter to uppercase (just like it is in his function names), puts the string "letter" on the front of it and adds the parentheses on the end. Executing this is just like executing the code "letterA()".

If the user enters more than one letter, the code just replaces the "a" with a "b" or "c" as needed:

But on the blinkytapes (a string of 60 LEDs) the letters are a function of their starting LED, like letterA(20).

We decided to write a letter for every 6 LEDs so we changed the code to

Python didn't like concatenating the strings to the integer x, so we changed x to a string:

This worked perfectly. Here's a picture of his blinkies. His classmate typed in "yolomcswag."