The Hunt for e

After a quick mini-course in Trigonometry during Monday's meeting of the Fun Calculus Program, the next installment will trace the discovery and development of the transcendental number e, which is around 2.7. My historical approach is of course influenced by Eli Maor's brilliant book e, Story of a Number, which explores e and its connection to logarithms, calculus, spirals and infinite series in fascinating detail.

I'm in the process of finding precalculus or calculus teachers who will allow me to observe their classes, because if textbooks are any indication, e is introduced as casually as breadsticks are plunked down on your table at Olive Garden. My suspicion is that most math teachers aren't aware of the rich history and applications that would make e more accessible and memorable. Even if teachers are aware, I'm sure entertaining such frivolous pursuits would cut into the time spent teaching 18th century tasks like estimating the roots of a polynomial.

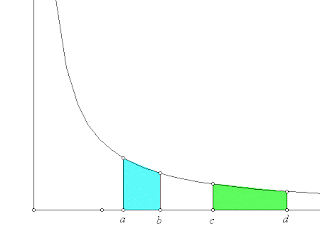
The truth is "The Hunt for e" was a real issue in the 1600s, after Fermat and others had figured out the pattern for finding areas under curves. The one curve that defied analysis was the hyperbola y = 1/x or x^-1, since using the area pattern would cause a zero denominator, which still frightens mathematicians in the 21st century. The curve definitely had an area underneath it, but finding a function to express it seemed impossible.

No less a genius than Newton took up the task and showed his skills by extending Pascal's triangle in a completely unexpected direction! He used his new invention, Calculus, to find an infinite series for the area under the hyperbola (a great way for a calculus teacher to introduce the need for such a seemingly unrelated idea) and was able to calculate the area with great precision.

Finding an actual function for the area took a similar step of logic, and many mathematicians had already noticed the area had a logarithmic quality: the area up to 2 plus the area up to 3 equals the area up to 6. Adding to multiply? How Scottish! After 20 years of painstaking drudgery performed by the Laird of Murchiston (who took time out of his busy schedule publishing Anti-Catholic propaganda to invent logarithms), astronomers and mathematicians were equipped with the 17-century equivalent of a TI-84. And they recognized the hyperbolic area problem as one of exponents. But what was the base of the exponents?

A seemingly harmless number already calculated by a bored banker who wondered how much money you'd make if you invested $1 at 100% interest for a year, compounded continuously.

It was the "compounded continuously" part that made e a most useful number for calculating populations (of people, animals and bacteria), temperatures, and in a few hundred years, amounts of radioactive material.

Quite a story!