Integration: Undoing All The Work We've Done

This week's topic in The Fun Calculus Program is Integration, which is the same pattern as differentiation, but backwards. It's similar to the way division is doing multiplication backwards: to find 18 divided by 3, you'd think, "What number do I have to multiply by 3 to get 18?" In the Galileo presentation we learned the derivative of x² is 2x, so the antiderivative (or "integral") of 2x is x².

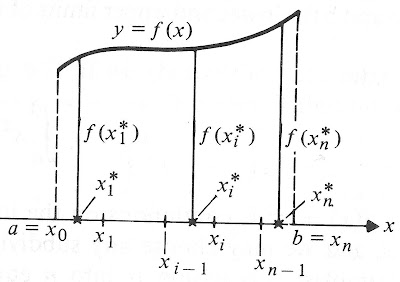
The Fun Calculus Program is the only calculus course I'm aware of where students are taught the Fundamental Theorem of Calculus in a way they'll actually remember. Everywhere else you're taught an algebraic proof, which might convince you not to question it. This snapshot from my college calc textbook suggests just how confusing the typical "proof" is, but aren't proofs supposed to clarify the situation?

Using graphing software, my students will actually experience the link between the area under the curve of a function and the antiderivative of the function. I start off graphing a horizontal line (in this case y = 3) and quickly find there's a pattern to the area under the line between 0 and x. It's always three times the ending x-value or y = 3x, so we graph that. That red line is the area function for the purple line y = 3.

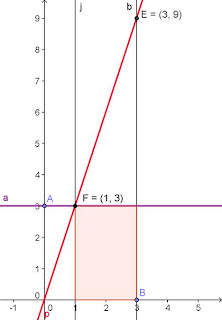
The Area Function is very handy for quickly and easily calculating the area under the purple line. The picture shows how to find the area between x = 1 and x = 3. Simply look at the red Area Function: read off the y-value at x = 3 and subtract the y-value when x = 1.

9 minus 3 is 6, which is the area we're looking for.

It just so happens the red Area Function is the antiderivative of the purple line. Coincidence? We then go on to investigate whether it works for diagonal lines and then parabolas, at which point the power of this "geometric proof" becomes evident.

I guarantee the participants in my Program remember the link between the area and the antiderivative at least as well as the average student in a calculus class who have to slog through the n, i, asterisk proof mentioned earlier.

Maybe better!