Into The Matrices

I remember working to keep my eyes open during a class in Business Math at Merrimack College; the awkward young professor was teaching us to solve 3x3 matrices using Gaussian Elimination. To this day I have no idea why matrices were included in the curriculum, but nobody ever lost their job making students do something called Gaussian Elimination.

Now I realize without that class I never would have appreciated the power and speed with which handheld calculators can solve even the nastiest matrix equation. A $50 TI or Casio calculator can handle matrices, but I wonder if any high school student can tell me why.

There certainly was one a few years ago, when I tutored a very nice high schooler named Carol whose teacher was making her class solve systems of equations in 3 variables. It's just like finding where two lines cross, but there are x's, y's and z's, like in this system:

10x + 5y + 2z =13

-13x – 4y + z = 3

17x + 3y – 2z = 1

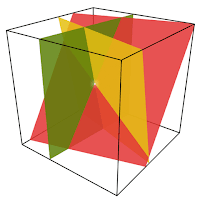
It looks a lot like the graphic on the left. The intersection of all 3 planes might be a line or a point. As you can imagine, using an algebraic method of solving this system would be very complicated, but it is assigned to the average high school algebra class.

Carol's class was one of those; she had more than one system to solve, so after we found out how laborious the solution would be I broke out the calculator.

If you make the coefficients of the unknowns into a 3x3 matrix A, and the constants on the right side of the equal sign a 3x1 matrix B, it makes an equation AX = B. "X" is the unknown 3x1 matrix containing the intersection of the system. Just like solving the equation 2x = 6 by dividing 6 by 2, to solve for the X matrix you have to multiply the B matrix by the inverse of the A matrix. In a calculator you would type in "A^-1 x B" but in Octave they have a special operator "\" you can use.

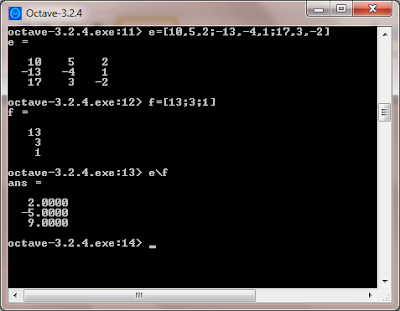
Today I put the above system into Octave. I'm not a computer expert, but I've learned just enough to get the answers I need. Here's what I did:

You can see the 3x3 matrix first, then the 3x1 matrix, then I "divided" to get the answers. The most laborious part of this solution was typing all the coefficients into the matrix in the right way. Computers are notoriously unforgiving to anyone using common sense instead of the manual to input stuff. You can see the solution where it says "ans = 2, -5, 9". Those are the values that work for x, y and z respectively in all the original equations.

I love technology. Using the same method I could solve a system of 10 equations with 10 variables with little more effort than it takes to type in the coefficients. Why can't they invent a scanner to do it?