The Square Root of the Square Root of -1

So your precalculus teacher tells you the square root of -1 is i. Did you ever ask her what the square root of i is? You'll either get a dirty look or an interesting exploration into complex numbers that will probably last twenty minutes into your lunch block.

As I said in the previous post, mathematicians learned they'd have to deal with the square roots of negative numbers as if they were just another letter in algebra. Eventually they reasoned that multiplying by -1 was like a 180 degree rotation around 0. Well, what if you did that in 2 steps?

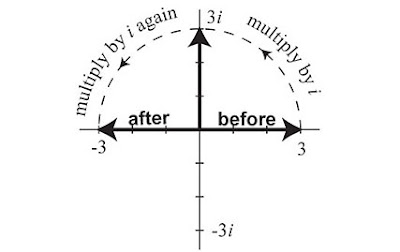
The vertical axis was renamed the imaginary axis, so complex numbers like a + bi could be expressed as points. Multiplying by the square root of negative one will get you halfway around, then multiplying again will get you the full 180 degrees. So multiplying by the square root of -1 is like a 90 degree rotation.

But what about the square root of i? That can be solved in a similarly geometric fashion. Just make the 90 degree rotation in two steps, each one being the square root of i. And each step will be a 45 degree rotation:

Using the 45-45-90 special triangle formula, the point is 1/sqrt(2) in the horizontal direction and 1/sqrt(2) in the vertical direction. 1/sqrt(2) is around .7071, and if you square 1/sqrt(2) + i/sqrt(2) you'll get i.

(1/sqrt(2) + i/sqrt(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i - 1/2 = i

Actually, if you did a rotation of 225 degrees twice you would rotate all the way around and back to 90 degrees, so that gives another square root of i.