Can you think of two numbers that give you the same result when you add them as when you multiply them? For example, 2 + 2 = 2 x 2, and there's another trivial solution, but are there any solutions to this when the numbers aren't the same? What if you include fractions or decimals?
Thursday, June 30, 2011
A Little Algebra
Tuesday, June 7, 2011
Series Join The Series
Newton's 1665 version of the calculus was different from the one we learn today: its essence was the manipulation of decimal expansions in arithmetic. The symbolic calculus...was also perfectly familiar to Newton, but apparently it was of only incidental interest to him. After all, armed with his power series, Newton could evaluate an integral like ∫ e-x2dx just as easily as ∫ sin x dx. Let Leibniz try that!That very integral (∫ e-x2dx) stumps most calculators, and I assume most students as well. But in the Series module participants in The Fun Calculus Program learn how to derive the series for ex, and simply substitute -x2 for x.
Saturday, February 12, 2011
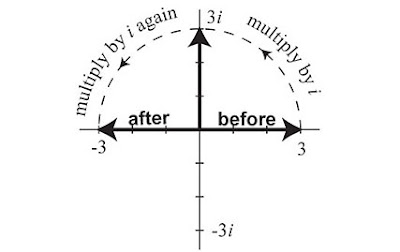
The Square Root of the Square Root of -1

Friday, February 11, 2011
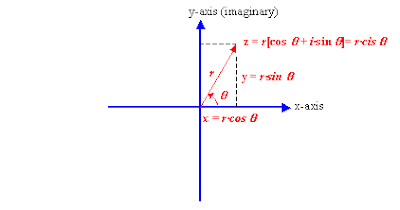
Trig Identities
Sunday, February 6, 2011
Did Euclid Exist?
"However, as Adelard of Bath, one of the first translators of the Elements, remarked, Muslims accepted reason, while authority prevailed in Christian Europe."
Possibly, the name “Euclid” was inspired by a similar translation error made at Toledo regarding the term uclides which has been rendered by some Arabic authors as ucli (key) + des (direction, space). So, uclides, meaning “the key to geometry”, was possibly misinterpreted as a Greek name Euclide.
Wednesday, February 2, 2011
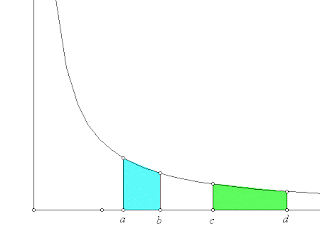
The Hunt for e
Sunday, January 30, 2011
I Finally Used Discrete Math!

ifelse numberofprongs = even[fd 400 rt 180 - 360 / numberofprongs][fd 400 rt 180 - 360 / (2 * numberofprongs)]
ifelse numberofprongs mod 2 = 0[fd 400 rt 180 - 360 / numberofprongs][fd 400 rt 180 - 360 / (2 * numberofprongs)]

Friday, January 28, 2011
Math Through Computer Programming
to neatorepeat 50 [square rt 5]end

Friday, January 21, 2011
Integration: Undoing All The Work We've Done
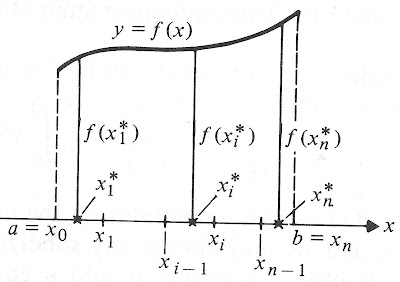
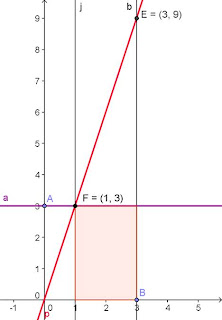
9 minus 3 is 6, which is the area we're looking for.
I guarantee the participants in my Program remember the link between the area and the antiderivative at least as well as the average student in a calculus class who have to slog through the n, i, asterisk proof mentioned earlier.
Tuesday, January 11, 2011
Into The Matrices
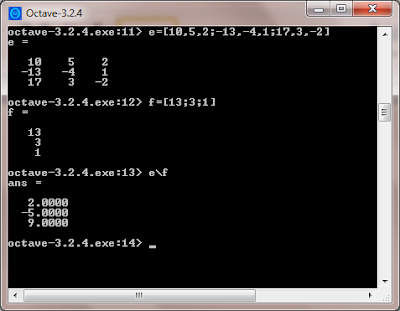
10x + 5y + 2z =13-13x – 4y + z = 3
17x + 3y – 2z = 1
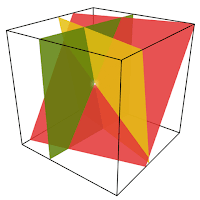
It looks a lot like the graphic on the left. The intersection of all 3 planes might be a line or a point. As you can imagine, using an algebraic method of solving this system would be very complicated, but it is assigned to the average high school algebra class.
Carol's class was one of those; she had more than one system to solve, so after we found out how laborious the solution would be I broke out the calculator.
If you make the coefficients of the unknowns into a 3x3 matrix A, and the constants on the right side of the equal sign a 3x1 matrix B, it makes an equation AX = B. "X" is the unknown 3x1 matrix containing the intersection of the system. Just like solving the equation 2x = 6 by dividing 6 by 2, to solve for the X matrix you have to multiply the B matrix by the inverse of the A matrix. In a calculator you would type in "A-1 x B" but in Octave they have a special operator "\" you can use.
Sunday, January 9, 2011
Physical Mathematics or Mathematical Physics?
Physical ideas can be real eye-openers and can suggest a strikingly simplified solution to a mathematical problem. The two subjects are so intimately intertwined that both suffer if separated. An occasional role reversal [physics serving math for a change] can be very fruitful, as this book illustrates. It may be argued that the separation of the two subjects is artificial.